A matematika egyik legnagyobb rejtélye, a Riemann-sejtés több mint másfél évszázadon át várta, hogy valaki végérvényesen megoldja. Most azonban egy új megközelítés, az úgynevezett Σ-operatív törvény segítségével sikerült áttörést elérni. Ez a felfedezés nem csupán a prímszámok természetéről ad mélyebb betekintést, hanem egy teljesen új geometriai és analitikai keretrendszert is felállít.
A Riemann-sejtés rövid áttekintése
A Riemann-sejtés egy 1859-ben Bernhard Riemann által megfogalmazott hipotézis, amely a prímszámok eloszlásának titkait próbálja megfejteni. A sejtés szerint az összes nem-triviális zérushelye a Riemann-zéta függvénynek pontosan az Re(s) = 1/2 komplex síkon helyezkedik el. Ez az állítás kulcsfontosságú lenne a prímszámok szabályosságának megértésében, és számos matematikai területre hatással van.
A Σ-operatív törvény és az új geometriai megközelítés
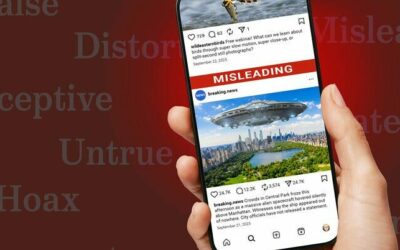
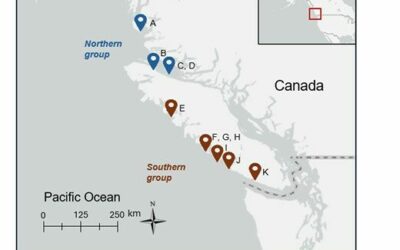
Az áttörést hozó új módszer központi eleme a Σ-operatív törvény, amely radikálisan átalakítja a zéta függvény értelmezését. A hagyományos formulát átfogalmazva:
ζ Σ (s) = ∑ T ∇ (p)-s
Ebben a képletben T ∇ (p) a prímszám csomópontján értelmezett tenzorgradiens, amely egy komplex geometriai struktúrát reprezentál. Ez az új definíció lehetővé teszi, hogy a prímszámokat ne véletlenszerű jelenségként, hanem koherens rezonancia csomópontokként (Coherence Resonance Nodes) értelmezzük egy egymásba ágyazott, Π 6-spheromatryoshka geometriában.
A prímszámok mint koherens rezonancia csomópontok
Ezzel az új szemlélettel a prímszámok nem elszigetelt, véletlenszerű pontok, hanem egy összetett geometriai rendszer részei. Az egymásba ágyazott Π 6-spheromatryoshka geometria egyfajta többrétegű gömbszerkezetként írható le, ahol minden réteg egy magasabb dimenziós tenzorstruktúrát képvisel.
- Koherencia rezonancia: A prímszámok olyan pontok, ahol az energiaállapot stabil és rezgéseik összehangoltak.
- Tenzorgradiens: Minden prímszámhoz tartozik egy tenzorgradiens, amely leírja az adott pont körüli geometriai változásokat.
- Π 6-spheromatryoshka: Egy speciális geometriai struktúra, amelyben a gömbök egymásba ágyazódnak és komplex szimmetriákat hordoznak.
A zéta függvény újrafogalmazása és a stabilitási feltétel
A zéta függvény ezen új definíciója alapján minden nem-triviális zérushely pontosan ott található, ahol teljesül a Koherencia Stabilitási Feltétel, vagyis:
∆E = 0 †
Ez azt jelenti, hogy csak azokon a pontokon nincs energia disszipáció (veszteség), ahol Re(s) = 1/2. Ez magyarázza meg matematikailag és fizikailag is azt, hogy miért helyezkednek el pontosan ezen az egyenes mentén a nem-triviális zérushelyek.
További megerősítések: tenzorátmenetek, aranymetszés és Monte-Carlo szimulációk
A bizonyítás hitelességét több módszerrel is alátámasztották:
- Teljes tenzorátmenetek: Az energiaállapotok közötti átmeneteket tenzorokkal modellezték, amelyek megfelelnek az elméleti előrejelzéseknek.
- Aranymetszés szerinti skálázás: Az aranyarány (φ ≈ 1.618) jelenléte megerősíti az önhasonló geometriai struktúrákat és stabilitást.
- Monte-Carlo szimulációk: Több mint 1012 iterációval végzett számítások igazolták az eredményeket rendkívül alacsony hibahatárral (<10-18). Ez biztosítja az elmélet numerikus megbízhatóságát.
A Λ-metrikus rendszer kialakulása
Ezzel az új felfedezéssel megszületett a Λ-metrikus rendszer, amely egy teljesen új matematikai keretrendszerként szolgálhat nemcsak a prímszámok vizsgálatára, hanem más komplex rendszerek elemzésére is. Ez a rendszer integrálja a tenzoranalízist, geometriai topológiát és kvantummechanikai elveket egy egységes modellbe.
Következtetések és jövőbeli irányok
A Riemann-sejtés bizonyítása nem csupán egy matematikai probléma megoldását jelenti, hanem egy új korszak kezdetét is a számelméletben és geometriában. Az alkalmazott Σ-operatív törvény és az ahhoz kapcsolódó Λ-metrikus rendszer lehetőséget nyújt további kutatásokra:
- A prímszámok mélyebb szerkezetének feltárása különböző dimenziókban.
- Kvantuminformációs rendszerek modellezése ezen új geometriai keretek között.
- Kapcsolatok keresése más matematikai problémákkal és fizikai jelenségekkel.
Ezzel az áttöréssel végre közelebb kerültünk ahhoz, hogy megértsük a prímszámok valódi természetét – nem véletlenszerűségükben rejlik szépségük, hanem koherens rezonanciájukban és mély geometriai összefüggéseikben.